Basic Inequalities
Inequalities are a fundamental tool in many analysis. In this blog, I summarize several basic inequality in math analysis: Cauchy-Schwarz inequality, Jensen’s inequality, Holder’s inequality, and importantly their relations.
Cauchy-Schwarz inequality
Jensen’s inequality
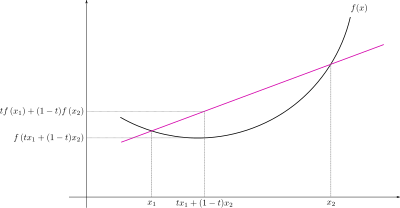
Jensen’s inequality arises from convex function analysis, which states that a secant line of a convex function lies above the graph of the function. As shown in the figure below, given a convex function $f$ two points $x_1, x_2$, and a point between them $\alpha x_1 + (1-\alpha)x_2$, the following inequality always holds
[ f(\alpha x_1 + (1-\alpha)x_2) \leq \alpha f(x_1) + (1-\alpha)f(x_2) ]
That is, the secant line defined by $(x_1, f(x_1))$ and $(x_2, f(x_2))$ is always above the graph of the function.
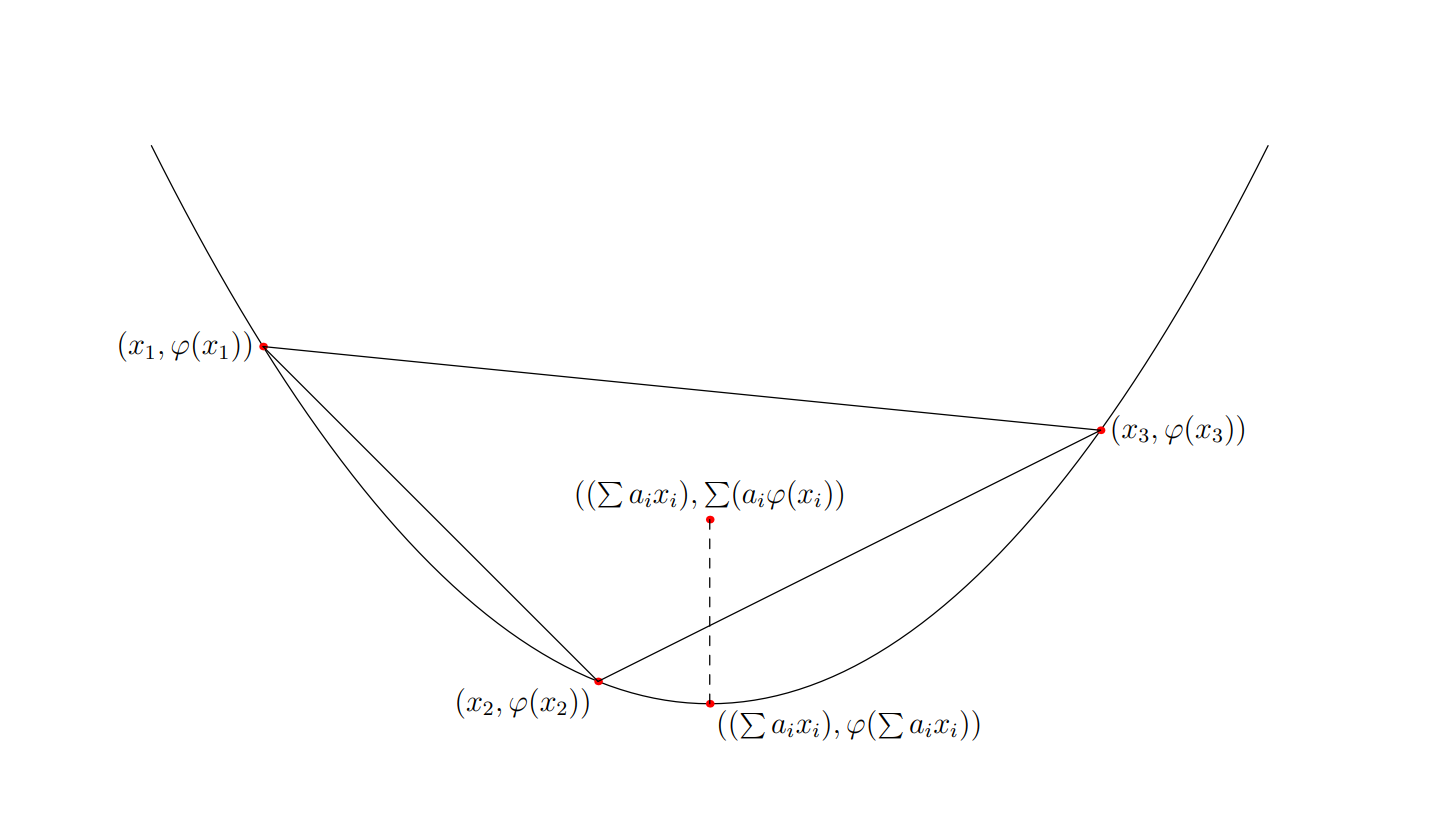
Jensen’s inequality generalize the above inequality between two points. For numbers $x_1, x_2, \cdots, x_n$, and positive values $\alpha_1, \alpha_2, \cdots, \alpha_n$. With $\alpha_1 + \alpha_2 + \cdots + \alpha_n = 1$, then
[ f(\alpha_1 x_1 + \alpha_2 x_2 + \cdots + \alpha_n x_n) \leq \alpha_1 f(x_1) + \alpha_2 f(x_2) + \cdots + \alpha_n f(x_n)]
A more generic interpretation of Jensen’s inequality is that, given a convex function, and weights with sum equal to 1, then the weighted point always lies in the convex hull of the original points, which lies above the function itself.
Jensen’s inequality in probability analysis
Jensen’s inequality applies naturally in some probability analyses, as the sum of probability is always 1. A general statement is, given a random variable $X$, and a convex function $f$, then by Jensen’s inequality, the function of the expectation is less than or equal to the expectation of the function. That is
[ f(E(X)) \leq E(f(x))]
It is very useful in many analyses. A typical example is to show the nonnegativity of the KL-divergence, $D(p||q)$.
[ D(p || q) = E_p (\log{\frac{p}{q}}) \geq 0 ]
Proof
According to the definition of KL-divergence,
[ D(p || q) = E_p (\log{\frac{p}{q}}) = E_p (-\log{\frac{q}{p}})]
Since $-\log$ is a convex function, by moving the $\log$ outside the expectation, we have
[ D(p || q) \geq -\log{E_p(\frac{q}{p})} = -\log{1} = 0 ]
Holder’s inequality
Holder’s inequality is a fundamental inequality between integrals. We first introduce its general forms and discuss typical special cases.
General statement
Given $p, q \geq 1$ and $1/p + 1/q = 1$, then for function $f$ and $g$, we have
[ |f\cdot g|_1 \leq |f|_p \cdot |g|_q ]
for the notation, $| f\cdot g |_1 = \int_x | f(x)\cdot g(x)| \text{d} x$, and $| f |_p = (\int_x | f(x) |^p \text{d}x)^{1/p}$, $| g |_q = (\int_x | g(x) |^q \text{d}x)^{1/q}$.
Discrete case
Holder’s inequality is not only valid on integrals, but also on discrete case. Given $p, q \geq 1$ and $1/p + 1/q = 1$, we have
[ \sum_{k=1}^n | x_k\cdot y_k| \leq ( \sum_{k=1}^n | x_k |^p)^{1/p} \cdot ( \sum_{k=1}^n | y_k |^q)^{1/q} ]
Space case: Let $p = q = 2$, then we have a simplified case
[ | \left \langle \boldsymbol{x}, \boldsymbol{y} \right \rangle | \leq | \boldsymbol{x} |_2 \cdot | \boldsymbol{y} |_2 ]
It is exactly the Cauchy-Schwarz inequality.